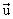 dans une base (
dans une base (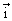 ,
, )
est l'unique couple de réels (x,y) vérifiant
)
est l'unique couple de réels (x,y) vérifiant
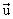 =x
=x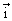 +y
+y .
Notation
.
Notation 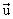 (x,y).
(x,y).C'est aussi le couple de coordonnées, dans le repère (O,
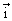 ,
, )
de l'unique point M tel que
)
de l'unique point M tel que  =
=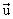 .
.composantes (d'un vecteur d'un plan) [latin : cum, avec ; et ponere, poser] (2) :
Le couple de composantes (ou coordonnées)
d'un vecteur 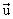 dans une base (
dans une base (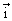 ,
, )
est l'unique couple de réels (x,y) vérifiant
)
est l'unique couple de réels (x,y) vérifiant
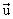 =x
=x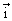 +y
+y .
Notation
.
Notation 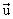 (x,y).
(x,y).
C'est aussi le couple de coordonnées, dans le repère
(O,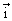 ,
, )
de l'unique point M tel que
)
de l'unique point M tel que  =
=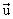 .
.

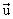 =3
=3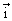 -2
-2 ,
donc le vecteur
,
donc le vecteur 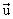 a pour composantes (3,-2) dans la base (
a pour composantes (3,-2) dans la base (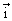 ,
, ).
).
composantes (d'un vecteur d'un plan) (2) :
Etant donnée une base (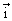 ,
, )
:
)
:
Si 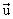 (x,y)
et
(x,y)
et  (x',y'),
alors
(x',y'),
alors 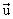 +
+ (x+x',y+y').
(x+x',y+y').
Si 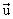 (x,y)
et k
(x,y)
et k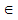
 ,
alors k
,
alors k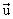 (kx,ky).
(kx,ky).
Etant donné un repère (O,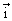 ,
, )
:
)
:
Si A(xA,yA) et B(xB,yB), alors 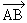 (xB-xA,yB-yA).
(xB-xA,yB-yA).