La normalité n'existe pas, sauf en mathématiques.
Synonyme de "orthogonal", utilisé dans certaines situations particulières, développées ci-dessous.
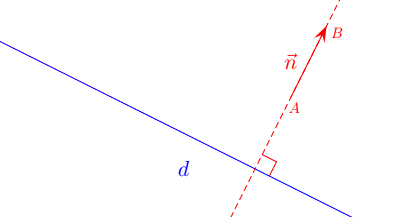
Le vecteur non nul \(\overrightarrow{n}=\overrightarrow{AB}\) est normal à la droite \(d\) si et seulement si \((AB)\) est perpendiculaire à \(d\).

περίμετρος
Deux droites sont parallèles si et seulement si elles admettent des vecteurs normaux colinéaires.
Deux droites sont perpendiculaires si et seulement si elles admettent des vecteurs normaux orthogonaux.
Le plan étant muni d'un repère orthonormé \((O,\overrightarrow{i},\overrightarrow{j})\) :
La droite d'équation \(ax+by+c=0\) admet \(\overrightarrow{n}\begin{pmatrix} a\\b\end{pmatrix}\) comme vecteur normal.
La droite d'équation \(y=mx+p\) admet \(\overrightarrow{n}\begin{pmatrix} -m\\1\end{pmatrix}\) comme vecteur normal.
Le vecteur non nul \(\overrightarrow{n}=\overrightarrow{AB}\) est normal au plan \(P\) si et seulement si \((AB)\) est orthogonale à \(P\), c'est à dire :
. à deux vecteurs de base de \(P\), ou :
. à deux vecteurs non colinéaires de \(P\).

\(\overrightarrow{n}\) est normal au plan \(P\) car il est orthogonal à \(\overrightarrow{u}\) et \(\overrightarrow{v}\), qui forment une base de \(P\).
Deux plans sont parallèles si et seulement si ils admettent des vecteurs normaux colinéaires.
Deux plans sont perpendiculaires si et seulement si ils admettent des vecteurs normaux orthogonaux.
Une droite est perpendiculaire à un plan si et seulement si l'un de ses vecteurs directeurs est normal au plan.
Le plan étant muni d'un repère orthonormé \((O,\overrightarrow{i},\overrightarrow{j})\) :
Le plan d'équation \(ax+by+cz+d=0\) admet \(\overrightarrow{n}\begin{pmatrix} a\\b\\c\end{pmatrix}\) comme vecteur normal.
Notion peu utilisée.
Le vecteur non nul \(\overrightarrow{n}=\overrightarrow{AB}\) est normal à la droite \(d\) si et seulement si \((AB)\) est orthogonale à d.