argument (d'un nombre complexe) [latin
: arguere, prouver] (T) :
 Soit
z un nombre complexe
non nul, et M son image dans le plan muni
d'un repère orthonormé
direct (O,
Soit
z un nombre complexe
non nul, et M son image dans le plan muni
d'un repère orthonormé
direct (O,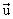 ,
, ).
).
Toute mesure en radian de l'angle (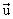 ,
, )
est un argument de z.
)
est un argument de z.
Un argument n'est donc défini qu'à un multiple
de 2π près.
Notation arg(z). (θ sur la figure ci-contre).
arg(1)≡0 [2π] ;
arg(i)≡ [2π] ;
arg(1
[2π] ;
arg(1 i)≡
i)≡ [2π].
[2π].
(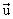 ,
,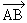 )≡arg(zB-zA) [2π].
)≡arg(zB-zA) [2π].
argument (d'un
nombre complexe) (T) :
Quels que soient les nombres complexes non nuls z et z', et l'entier
relatif n :
arg(z)≡0 [π] ⇔
z est réel.
arg(z)≡0 [2π] ⇔
z est un réel positif.
arg(z)≡ [π] ⇔ z est
imaginaire pur.
[π] ⇔ z est
imaginaire pur.
arg( )≡-arg(z) [2π]
)≡-arg(z) [2π]
arg(-z)≡ arg(z)+π [2π]
arg(- )≡π-arg(z)
[2π]
)≡π-arg(z)
[2π]
arg(zz')≡arg(z)+arg(z') [2π]
arg(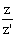 )≡arg(z)-arg(z') [2π]
)≡arg(z)-arg(z') [2π]
arg(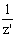 )≡-arg(z') [2π]
)≡-arg(z') [2π]
arg(zn)≡n arg(z) [2π]

 Soit
z un nombre complexe
non nul, et M son image dans le plan muni
d'un repère orthonormé
direct (O,
Soit
z un nombre complexe
non nul, et M son image dans le plan muni
d'un repère orthonormé
direct (O,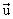 ,
, ).
).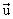 ,
, )
est un argument de z.
)
est un argument de z. [2π] ;
arg(1
[2π] ;
arg(1 i)≡
i)≡ [2π].
[2π].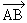 )≡arg(zB-zA) [2π].
)≡arg(zB-zA) [2π].