Gauss [Carl Friedrich Gauss, mathématicien allemand (1777-1855)] (1)(T) :

Méthode du pivot de Gauss pour la résolution des systèmes d'équations linéaires (1)

Méthode consistant à transformer un système en un système triangulaire équivalent. Elle s'appuie sur le théorème suivant :
Les transformations suivantes fournissent un système équivalent à un système donné :
  Multiplier les deux membres d'une ligne par le même réel non nul.
Remplacer une ligne par la somme ou la différence de cette ligne et d'une autre.

Pour faciliter la lecture, les codages suivants sont utilisés :
Li ième ligne
aLi ième ligne multipliée par a
Li + Lj somme de la ième ligne et de la jème ligne
Li - Lj différence de la ième ligne et de la jème ligne
Li Lj remplacement de la ième ligne par la jème ligne

Les transformations permises par le théorème de Gauss s'écrivent donc, sous forme codée :
LiaLi, (a≠0)
LiLi + Lj ou LiLi - Lj, (i≠j)

Pour écourter, ces deux transformations se font souvent en même temps, soit :
LiLi ± aLj (a≠0, i≠j)

La stratégie consiste alors à :
1) Éliminer une inconnue dans deux lignes en utilisant la troisième (appelée pivot).
2) Éliminer une autre inconnue dans l'une de ces deux lignes en utilisant l'autre.

Soit à résoudre S⇔.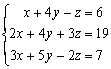
1) Éliminer x dans L2 et L3 en utilisant comme pivot L1 :
S⇔⇔.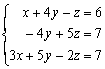
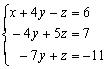
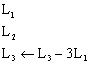2) Éliminer z dans L2 en utilisant comme pivot L3 :
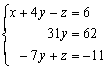
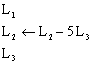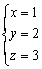⇔. S={1,2,3}.

Théorème de Gauss (T)

Soit a, b et c trois entiers.
Si a divise bc, et est premier avec b, alors a divise c.

Courbe de Gauss (T)

Courbe représentative de la fonction x (dite aussi courbe en cloche), densité de la loi de probabilité normale centrée réduite sur .