similitude [latin
: similis, semblable] (T) :
Une similitude plane est une application
du plan sur lui même qui multiplie les distances par un réel
strictement positif, appelé rapport de la similitude :
il existe un réel strictement positif k tel que pour tout couple de points
M et N : M'N'=kMN.
Une similitude est directe lorsqu'elle conserve les angles orientés.
Visualisation.
Une similitude est indirecte lorsqu'elle change un angle orienté en son
opposé. Visualisation.
Une homothétie de rapport k est
une similitude directe de rapport |k|.
Une réflexion est une similitude
indirecte de rapport 1.
similitude (T) :
Toute similitude directe de rapport k est la composée
d'une homothétie de rapport k et
d'un déplacement.
Dans le plan muni d'un repère orthonormé  ,
l'expression analytique de la similitude de centre O, de rapport k et d'angle
,
l'expression analytique de la similitude de centre O, de rapport k et d'angle
 est
est
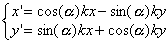 .
.
Ecriture complexe d'une similitude directe : z'=az+b, avec |a| 0.
0.
Toute similitude indirecte de rapport k est la composée
d'une homothétie de rapport k et
d'un antidéplacement.
Ecriture complexe d'une similitude indirecte : z'=a +b,
avec |a|
+b,
avec |a| 0.
0.