homothétie [grec : homos, semblable ; et thesis, action de poser] (1) :

Soit O un point et k un réel non nul. L'homothétie de centre O et de rapport k est la fonction : MM', où M' est le point défini par =k. Notation : h_O,k (ou simplement h lorsqu'il n'y a pas de confusion possible).

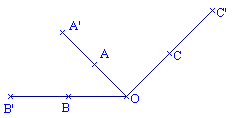Sur la figure ci-contre, A' est l'image de A par l'homothétie de centre O et de rapport 2 car =2.
De même B' et C' sont les images respectives de B et C par l'homothétie de centre O et de rapport 2.

Une homothétie de rapport -1 est une symétrie centrale.

homothétie (1) :

Si A'=h_O,k(A) et B'=h_O,k(B), alors =k.

Par une homothétie, l'image d'une droite est une droite qui lui est parallèle.

Une homothétie conserve les angles du plan orienté.

Une homothétie conserve les intersections : si E et F sont deux figures, h(E∩F)=h(E)∩h(F).

Dans le plan muni d'un repère (O,,) l'expression analytique de l'homothétie de centre Ω(a,b) et de rapport k est .

Une homothétie est une transformation.

La composée de deux homothéties de rapports k et k' est une homothétie de rapport kk'.
La composée d'une homothétie et d'une translation est une homothétie.