cotangente (d'un réel) [latin : cum, avec et tangere, toucher] (2) :

Dans le plan muni d'un repère orthonormé direct (O,,), soit I le point de coordonnées (1;0), J le point de coordonnées (0,1) et d la tangente en J au cercle trigonométrique.
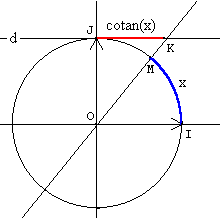
Soit x un réel. Soit M le point du cercle trigonométrique tel que x soit une mesure en radians de l'angle (,) (en bleu), et K le point d'intersection des droites d et (JM) (s'il existe). Par définition, cotan(x) est la mesure algébrique de JK (rouge). Elle est donc définie pour x0 modulo .

cotan()=, cotan()=1, cotan()=0 .

cotangente (d'un réel) (2) :

La cotangente d'un réel est égale au quotient de son cosinus par son sinus : pour x0 modulo , cotan(x)=.
La fonction cotangente est dérivable sur son ensemble de définition et pour x0 modulo , cotan'(x)=-1-cotan²(x)=-.