La réunion des ensembles \(A\) et \(B\) est l'ensemble des éléments qui appartiennent à \(A\) ou à \(B\).
Notation : \(A\cup B\).
C'est l'ensemble des éléments qui appartiennent à au moins l'un des ensembles \(A\) et \(B\).
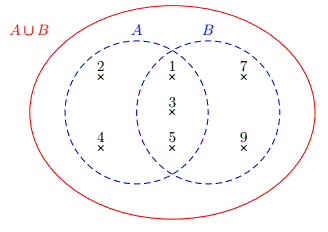
Soient \(A=\{1,2,3,4,5\}\) et \(B=\{1,3,5,7,9\}\). Alors \(A\cup B=\{1,2,3,4,5,7,9\}\).

Diagramme de Wenn de la situation.
1. \(A\) et \(B\) étant deux sous-ensembles d'un ensemble fini \(E\) : \[Card(A\cup B)=Card(A)+Card(B)-Card(A\cap B).\]
2. Dans l'ensemble des parties d'un ensemble \(E\) :
2.1. la réunion est commutative : quelles que soient les parties \(A\) et \(B\) de \(E\), \(A\cup B=B \cup A\)
2.2. la réunion est associative : quelles que soient les parties \(A\) et \(B\) de \(E\), \((A\cup B)\cup C=A \cup (B \cup C)\).
2.3. la réunion est distributive par rapport à l'intersection : quelles que soient les parties \(A\) et \(B\) de \(E\), \(A\cup (B\cap C)=(A \cup B) \cap (A \cup C)\).