 .
.
Soit λ un réel strictement positif.
Une variable aléatoire X suit une loi exponentielle de paramètre λ sur l'intervalle [0,+∞[ si et seulement si sa densité de probabilité est la fonction définie sur [0,+∞[ par f(t)=λe-λt.
Notation : X∼exp(λ).
Soit X une variable aléatoire qui suit une loi exponentielle de paramètre λ sur l'intervalle [0,+∞[. Alors :
Pour tous u et v tels que 0≤u<v : P(u<X<v)=e-λu-e-λv.
La fonction de répartition de X est la fonction définie sur ]a,b[ par : φ(x)=1-e-λx.
L'espérance de X est E(X)=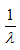 .
.
La médiane de X est m=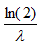 .
.